相對論和張量分析 – Coordinate Covariant, Contravariant, Invariant (座標系協變，逆變，不變)

by allenlu2007

黎曼微分幾何是廣義相對論的數學基礎。張量分析是黎曼微分幾何的必備數學工具。

黎曼幾何是彎曲幾何(curved geometry)，不同於歐式平直幾何(straight geometry)。
黎曼幾何研究內稟(intrinsic)的特性以及嵌入(embedded)歐式幾何的特性。例如 2D Swiss Roll 的內稟幾何特性和一張平紙無異 (i.e. intrinsic curvature = 0), 但是 embedded 在高維(3D)歐式空間卻有曲率。

由於相對論的影響，不同（運動）觀察者所量測的物理定律 (e.g. least action principle) 都要一樣。這剛好對應幾何不同座標系的“不變性”。不變的 scalar 可以使用 invariant. 不變的 vector/tensor, 因為分量仍然和座標系相關，我們用 covariant 表述。

觀察者和座標系容易混淆的重點：

不同（運動）觀察者對應幾何不同座標系. 不要執著一個是動態，一個是靜態。這裏所說的幾何座標系都包含時間軸 ( $t$ -axis), 從下到上代表過去到未來。任何運動都可以用一條靜態的世界線（worldline) 表示。
一條 wordline 是相對於一個觀察者（座標系）。例如 A 觀察到一個靜止物體 S，在 A 的（直角）座標系 S 的位置就是一條垂直的 world line. B 是一個相對 A 定速 $v$ 移動的觀察者。B 要如何得到 S 的 world line?

有兩個方法：

(i) B 創造自己的（直角）座標系以及 S 的 world line. 顯然在 B 的直角座標系 S world line 是一條斜線。斜率是 $-v$ (assuming $v \ll c$ ). 兩個不同的直角座標系 for S 運動，對應 A 和 B 觀察者 (observer oriented)。這不是我們所要的。如果有無窮多觀察者（等速或等加速觀察者）就需要無窮多直角座標系以及無窮多的 world lines for the same S 的運動。
我們關心 S 的運動 (object oriented) 一次看到 A 和 B 座標系的詮釋，見 (ii). 這對廣義相對論研究時空內稟幾何特性很重要。

(ii) 在 A 的直角座標系 (grid line) 重劃 B 的（非直角）座標系 (grid line)。同一條垂直的 world line, 在 A 座標系 grid line 是靜止；但在 B 座標系 grid line 則是運動。
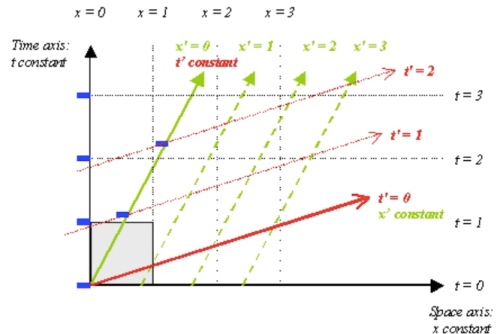
下圖是一個例子。A 觀察者是直角座標系 $(x, t)$ , 網格線 (grid line) 是正方形。但對 B 觀察者（相對速度為 $v$ ）對應座標系 $(x', t')$ , 網格線是平行四邊形。此處是用 Lorentz 變換，所以 $t'=0,1,2$ 格線是斜線。如果是 Galilean 變換， $t'=0,1,2$ 會是水平線。對於 A 的靜止物體 S, 其 world line 就是 $x=0$ 垂直線。對 B 座標系 $(x',t')$ 而言， $x=0$ 垂直線 world line 對應一個後退的運動。
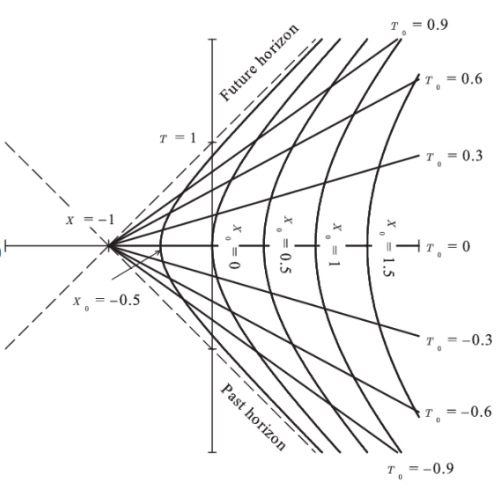
注意這種重劃座標系網格並不限於相對速度固定的觀察者。原則上適用任何運動觀察者。假設觀察者 C 是相對于 A 有固定等加速度。也可以定義 $(x'', t'')$ 網格線。下圖是 Lorentz 變換 C 的座標系。 $x''=const$ 變成雙曲線。 $t''=const$ 變成聚集在 $x''=-1$ 的投射線 (假設光速=1). 網格線變成更奇怪的四邊形。注意在 Lorentz transform 所有速度無法超越光速。觀察者 C 無法持續加速超越光速。 Galilean 變換 C 的座標系則不同。 $x''=const$ 變成拋物線。 $t''=const$ 還是水平線。

回到物理和幾何的對照：

運動的物體 $\iff$ 幾何的一條世界線 C (不是面或其他形狀)
不同慣性運動或是非慣性運動觀察者 $\iff$ 幾何的不同座標系以及網格
狹義相對論：物理定律在不同慣性座標系不變 (scalar:invariant; vector/tensor:covariant)
廣義相對論：物理定律考慮等效原理在不同座標系不變
物理定律 $\iff$ 幾何不變量（如何對應 scalar: invariant; tensor: covariant）
- 微分幾何的 1st fundmental form $ds^2 = c^2 dt^2-dx^2-dy^2-dz^2 = c^2 dt'^2-dx'^2-dy'^2-dz'^2$ 幾何量是微分弧長 coordinate invariant 對應物理的 Lorentz transform. 如果少了 $c^2 dt^2$ 就是 (-1)*Galilean transform.
- 注意微分幾何的 1st fundamental form 可以推廣到 curved space or coordinate. 這裏使用愛因斯坦 summation notation. $ds^2 = g_{\alpha\beta}{dx^\alpha}{dx^\beta}$
- 牛頓第二定律: $\vec{F} = m\vec{a} \,$ 在 Galilean transform 不變。因為是 vector, vector components 在不同座標系不同，稱為 covariant. 對應的幾何不變量是“curvature vector". 但在 Lorentz transform, $\vec{F} \,and\, \vec{a}$ 甚至不是 4-vector/tensor, 連 covariant 也不是。如何得到符合 Lorentz tranform 4-vector/tensor 的力學定律呢？下面描述。
- 最小作用力原理 (Least action principle) 是比牛頓運動定律更基本的定理。分析力學首先找到 Lagrangian $L$ (單位是能量)，differential action $dS = L dt$ (單位是能量*時間，大自然兩者都要省)。Total action 就是空間兩點 $(p_1, p_2)$ 和時間兩點 $(t_1, t_2)$ 路徑積分。最小作用原理用變分法找到最小 $S$ 的路徑。 $S = \int_{t_1}^{t_2} L dt$
- 舉一個例子：古典力學 Lagrangian of free particle (no potential field) in Cartesian and polar coordinate. [@ActionPhysics2019]
  
  $latex L =\frac{1}{2} m v^2=\frac{1}{2} m (\dot{x}^2 + \dot{y}^2)
  \quad L =\frac{1}{2} m (\dot{r}^2 + r^2 \dot{\varphi}^2) $
- 最小作用原理推廣到 4D 時空 for two events $(x_1, x_2, x_3, x_4)$ and $(x'_1, x'_2, x'_3, x'_4)$ . 因為時間 $t$ 已經變成 $x_1$ , 需要用 dummy variable $\lambda$ . 上述的 $S$ 公式完全適用。
- 但在相對論力學 4D 時空的 Lagrangian of free particle (no potential field). [@RelativisticLagrangian2019] $L = -\frac{m_o c^2}{c} \sqrt{g_{\alpha\beta}\frac{dx^\alpha} {d\lambda}\frac{dx^\beta}{d\lambda}} = -\frac{m_o c^2}{c} \frac{ds}{d\lambda} \\ \approx m_o c^2 + \frac{1}{2} m_o v^2! \quad \text{assuming } v \ll c$ $g_{\alpha\beta}$ 沒有單位。根號的單位是速度，和光速 $c$ 單位抵銷。 $m_o c^2$ 的單位是能量。所以 $L$ 的單位在 4D 時空仍然是能量。 $\lambda$ 只是 dummy variable (時間單位)。 $ds$ 是 1st fundmental form 的根號，或是微分弧長。滿足 Lorentz transform invariant. In a word, $L$ 對應幾何量是弧速。 $S = \int L d\lambda = \int -\frac{m_o c^2}{c} \sqrt{g_{\alpha\beta}\frac{dx^\alpha} {d\lambda}\frac{dx^\beta}{d\lambda}} d\lambda$ 重點是 S (action) 對應的是 4D 時空兩點之間的總弧長 (with a proportional constant). 最小作用原理對應幾何量是兩點之間最短距離的弧線，稱為 geodesic (測地線或地直線) which is coordinate invariant. [@cyrilGeodesicEquation2018] 也就是說，不同慣性運動的觀察者的最小作用原理都是一樣。但如何推廣到非慣性觀察者？

UTM. 2018. “Proper Time, Coordinate Systems, Lorentz Transformations | Internet Encyclopedia of Philosophy.” 2018. https://www.iep.utm.edu/proper-t/.

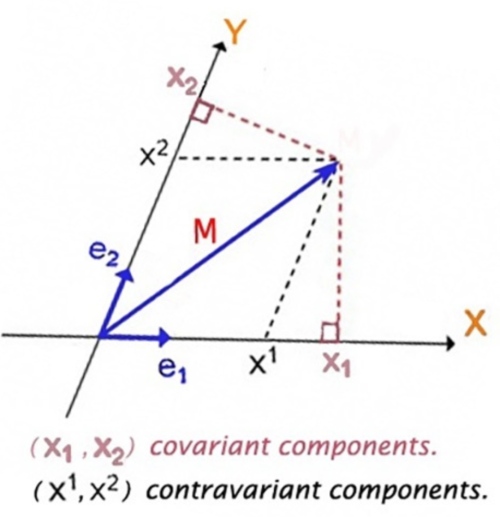
Coordinate Invariant, Covariant, Contravariant

Coordinate invariant 基本是 scalar quantity or field, 例如 $ds$ , geodesic, scalar curvature, etc.

Contravariance 基本是 vector/tensor, 例如 curvature tensor, …. 什麼是 contravariant? $(A^x e_x)$ base vector $(e_x)$ 變大，component $(A^x)$ 變小。所以是 contra-variance.

Covariance 也是 vector/tensor, 為什麼是 covariance? 一個例子是 gradient of scalar field. $(\frac{\partial f}{\partial x} e^x, \frac{\partial f}{\partial y} e^y, \frac{\partial f}{\partial z} e^z)$ , base vector $e^x$ 越大， component 也越大。

Covariance and Contra-variance of Vector/Tensor

歐式空間（或是 tangent space on manifold）

如何在座標系表達一個向量 $\vec{v}$ ?
選擇一組 basis vectors (假設不正交). 然後分解成 basis vectors 的平行分量 (下圖右 typo $v_x \to v^x \,\,and\,\, v_y \to v^y$ )。
$\vec{v} = v^x \mathbf{e_x}+v^y \mathbf{e_y}$
我們稱 $v^x$ and $v^y$ contra-variance, 因為 $v^x \,,v^y$ 和 $\mathbf{e_x} \,,\mathbf{e_y}$ 是反比的關係。
問題是如何用數學式計算 $v^x$ and $v^y$ ? （見下文）
如果是在直角座標系如下，可以看出 contra-variant!

$v^x = \frac{\vec{v} \cdot e_x}{\lVert\mathbf{e_x}\rVert^2} \quad v^y = \frac{\vec{v} \cdot e_y}{\lVert\mathbf{e_y}\rVert^2}$

顯然在非直角座標系是錯的！正確的數學表述在後面。

此時稱 $\mathbf{e_x} \,,\mathbf{e_y}$ (tangent) basis vectors 可以使用 Einstein summation notation:
$\vec{v} = v^x \mathbf{e_x}+v^y \mathbf{e_y}= v^i \mathbf{e_i}\quad \text{or } v^i \text{ in short}$

下一個問題，是否還有其他方法表示一個向量？Yes!
我們可以用垂直投影分量表示一個向量 (下圖左, $v_x = \vec{v} \cdot e_x \,\, v_y = \vec{v} \cdot e_y$ ).
我們稱 $v_x$ and $v_y$ covariance, 因為 $v_x \,,v_y$ 和 $\mathbf{e_x} \,,\mathbf{e_y}$ 是正比的關係。
$\vec{v} = v_x \mathbf{e^x}+v_y \mathbf{e^y}= v_i \mathbf{e^i} \quad \text{or } v_i \text{ in short}$

問題是如何找到對應的 (cotangent) basis vector $e^x$ and $e^y$ ?

為了滿足 $v_x = \vec{v} \cdot e_x$ 和 $v_y = \vec{v} \cdot e_y$ ，可以得出 $e^i e_j = \delta^i_j$ !
也就是說 $e^x \perp e_y \,, e^y \perp e_x$ . 同時 normalize $e^x e_x = e^y e_y = 1$ . 也就是反矩陣關係！

注意 $e^x \nparallel e_x \,, e^y \nparallel e_y$ 除非 $e_x \,, e_y$ 是直角座標系。

此時可以用新的 (cotangent) basis vector 表示：
$\vec{v} = v_x \mathbf{e^x}+v_y \mathbf{e^y}= v_i \mathbf{e^i} = v^i \mathbf{e_i}$

$v_x = \vec{v} \cdot e_x \quad v_y = \vec{v} \cdot e_y \quad or \quad v_i = \vec{v} \cdot e_i$

$v^x = \vec{v} \cdot e^x \quad v^y = \vec{v} \cdot e^y \quad or \quad v^i = \vec{v} \cdot e^i$

因為 $e^i$ 和 $e_i$ 是反比。 $e_i$ 越大， $e^i$ 越小， $v^i$ 就愈小，稱為 contra-variance. 但是 $v_i$ 卻是愈大，和 $e_i$ 正比，稱為 covariance.

Inner Product Using Einstein Notation
$\vec{u} \cdot \vec{v} = u^i \mathbf{e_i} v_j \mathbf{e^j} = u^i v_j \delta^i_j = u^i v_i = u_i v^i \\ = u^i \mathbf{e_i} v^j \mathbf{e_j} = u^i v^j g_{ij} = u_i v_j g^{ij}$

Scalar field is invariant.
Vector/tensor field is contravariant.
Gradient of scalar field is a vector field, which is co-variant.

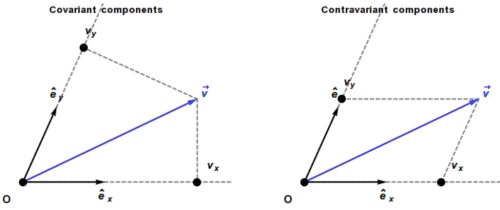
https://www.quora.com/What-are-%E2%80%9Ccovariant%E2%80%9D-and-%E2%80%9Ccontravariant%E2%80%9D-vectors-as-intuitive-representations

為了直觀了解 curved coordinate and space, 用以下的順序理解：直角座標系 $\to$ 斜角座標系 $\to$ 歐式空間極座標系 (curved coordinate) $\to$ 球面座標系 (curved space)

orthonormal 座標系
$e^1 = (1, 0) \,\, e^2= (0, 1)$
$e_1 = (1, 0) \,\, e_2= (0, 1)$
scaled 座標系
$e^1 = (a, 0) \,\, e^2= (0, b)$
$e_1 = (\frac{1}{a}, 0) \,\, e_2= (0, \frac{1}{b})$
Non-orthogonal 座標系
$e^1 = (a, 0) \,\, e^2= (d, b)$
$e_1 = (\frac{1}{a}, \frac{-d}{ab}) \,\, e_2= (0, \frac{1}{b})$
Polar 座標系 $(r,\theta) \to (dr, r d\theta)$
$e^1 = (a, 0) \,\, e^2= (0, b)$
$e_1 = (\frac{1}{a}, 0) \,\, e_2= (0, \frac{1}{b})$

三維空間
推廣上述二維的垂直觀念到三維空間。
$e^1$ 的方向是由 $e_2 \,, e_3$ 所形成平面的法線 (normal) 決定，i.e. $e^1 e_2 = e^1 e_3 = 0$ .

$e^1$ 的大小是由 $e_1$ 決定，i.e. $e^1 e_1 = 1$

同理 $e^i$ 的方向是是由 $e_j \,, e_k$ 所形成平面的法線 (normal) 決定。 $e^i e_j = \delta^i_j$

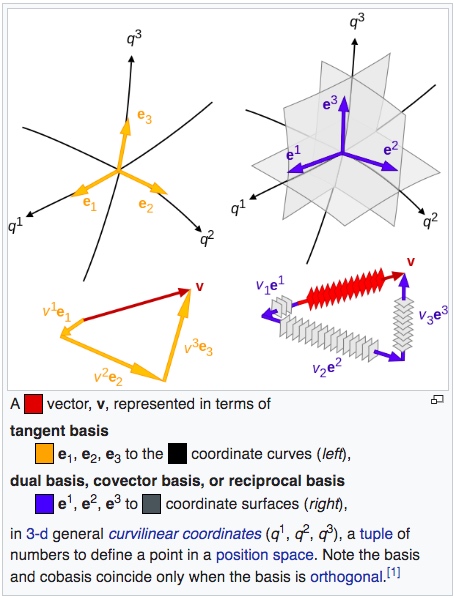
推廣到 n 維空間：
Tangent basis: e1, e2, …, en, C(n,1)=n
Reciprocal basis: e1.,… C(n, n-1) = n

Curved Space or Coordinate System
Basis Vector $(e_1, e_2, ...)$
Reciprocal Basis Vector $(e^1, e^2, ...)$
$e_i e_j = g_{ij}$ metric tensor g matrix
$e^i e^j = g^{ij}$ inverse metric tensor, 真的是 inverse g matrix.
$e^i = g^{ij} e_j \quad\quad e^i e_k = g^{ij}e_j e_k = g^{ij}g_{jk} = \delta^i_j$

Covariant Derivative of Scalar Field and Vector Field

Covariant derivative 是 directional derivative 的推廣。同樣用以下的順序理解：直角座標系 $\to$ 斜角座標系 $\to$ 歐式空間極座標系 (curved coordinate) $\to$ 球面座標系 (curved space)

Scalar field: $f(x, y)$ on orthonormal 座標系
$e^1 = (1, 0) \,\, e^2= (0, 1)$
$e_1 = (1, 0) \,\, e_2= (0, 1)$
$\nabla f = \frac{\partial f}{\partial x} e^x + \frac{\partial f}{\partial y} e^y$
Scalar field: $f(x, y)$ on scaled 座標系
$e^1 = (a, 0) \,\, e^2= (0, b)$
$e_1 = (\frac{1}{a}, 0) \,\, e_2= (0, \frac{1}{b})$
$\nabla f = \frac{\partial f}{\partial x} e^x + \frac{\partial f}{\partial y} e^y$
Scalar field: $f(r, \theta)$ on 極座標系
$e_i\cdot e_j = g_{ij}$ , $e^i\cdot e^j = g^{ij}$ , $e_i\cdot e^j = \delta_{ij}$ .
$e_i = g_{ij} e^j$ , $e^i = g^{ij} e_j$
$ds^2 = dr^2 + r^2 d\theta^2 = g_{ij}dx^idx^j$
$g_{ij}=\left(\begin{array}{cc}{g_{rr}=1} & {g_{r\theta}=0} \\ {g_{\theta r}=0} & {g_{\theta\theta}=r^2}\end{array}\right) \,\, g^{ij}=\left(\begin{array}{cc}{g^{rr}=1} & {g^{r\theta}=0} \\ {g^{\theta r}=0} & {g^{\theta\theta}=\frac{1}{r^2}}\end{array}\right)$
$\det(g_{ij})=|g|= r^2$ , $\det(g^{ij})=|g|^{-1}=1/r^2$
$latex \nabla f(r,\theta) = \frac{\partial f}{\partial r} e^r + \frac{\partial f}{\partial \theta} e^\theta \quad\text{(1- form, covariant)}\\
= \frac{\partial f}{\partial r} e_r + \frac{1}{r^2}\frac{\partial f}{\partial \theta} e_\theta \qquad\text{(contra-variant)} $

另外常見的表示法是 Euclidean metric, normalized form, $|g|=1$ :
$\nabla f(r,\theta) = \frac{\partial f}{\partial r} \hat{e}_r + \frac{1}{r}\frac{\partial f}{\partial \theta} \hat{e}_\theta$

一個純量場（0階張量）的梯度, $\nabla \phi$ , 是一個向量。更準確的說是一個一階張量(1-form)。在求方向導數或是散度都很方便。
一個一維量場的梯度, $\nabla \phi$ , 是一個二階張量(index 在樓上和樓下)。以此類推。

重新回到物理和幾何的對照

(三維空間 + 一維時間): 滿足 Galilean tranform. $F = ma$ , 最小作用原理~?。
四維時空：滿足 Lorentz tranform. 最小作用原理 $\iff$ Geodesic.
(n-維空間 + 一維時間)：多粒子運動。constrain 變為 manifold. Tangent space (contra-variant basis): Lagrangian mechanics. Cotangent space (co-variant basis): Hamiltonian mechanics. How to expand this?

Reference

Wiki. 2019. “Covariance and Contravariance of Vectors.” In Wikipedia.
https://en.wikipedia.org/w/index.php?title=Covariance\_and\_contravariance\_of\_vectors&oldid=904269873

“Action (Physics).” 2019. Wikipedia.
https://en.wikipedia.org/w/index.php?title=Action_(physics)&oldid=904671703

Cyril. 2018. “Geodesic Equation from the Principle of Least Action.” September 18, 2018.
http://einsteinrelativelyeasy.com/index.php/general-relativity/97-geodesic-equation-from-the-principle-of-least-action.

“Relativistic Lagrangian Mechanics.” 2019. Wikipedia.
https://en.wikipedia.org/w/index.php?title=Relativistic_Lagrangian_mechanics&oldid=884947845

Appendix

Example 1: 牛頓空間以及不同慣性運動觀察者

3D 歐式空間 + 1D 時間 (空間時間各自獨立，互不影響)
不同慣性觀察者：
- $x' = x - v t$
- $t' = t \,\,;\,\, y' = y \,\,;\,\, z' = z$
- $(x,y,z,t)$ 座標系。為了簡化在 2D plan，只考慮 $(x, t)$ . 垂直軸是 $t$ 軸。
- 靜止在原點的物體。它的 world line 是一條垂直線
對應座標轉換：x' = constant grid line 變成斜線，斜率由速度決定
物理定律不變 (invariant)： $F = m a = m \ddot{x} = m \ddot{x'}$

Example 2: 狹義相對論慣性運動觀察者

空間：4D 閔式幾何 (Minkovsky space-time 4D space)
運動方程式：least action principle <-> geodesic
不同慣性觀察者： y = x – v*t

Example 2: 廣義相對論