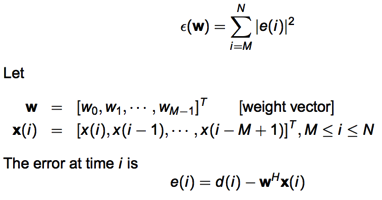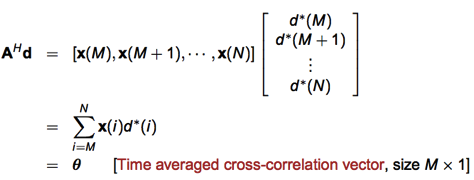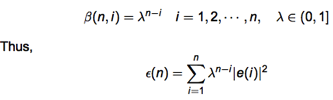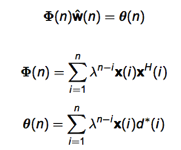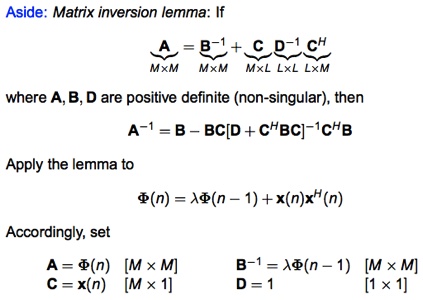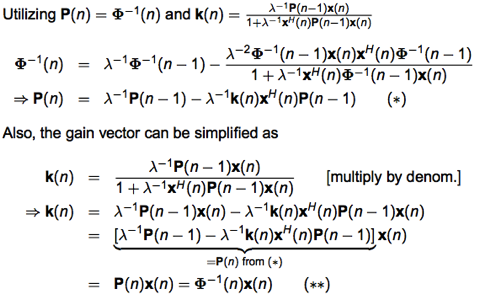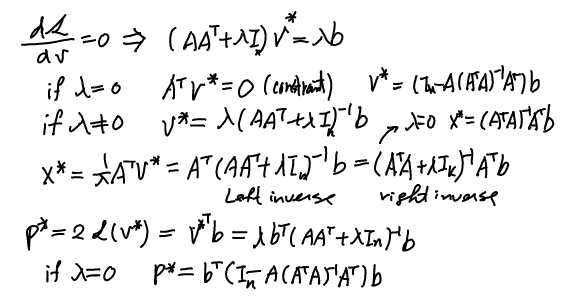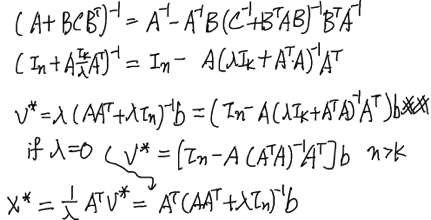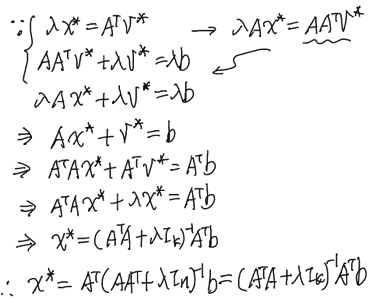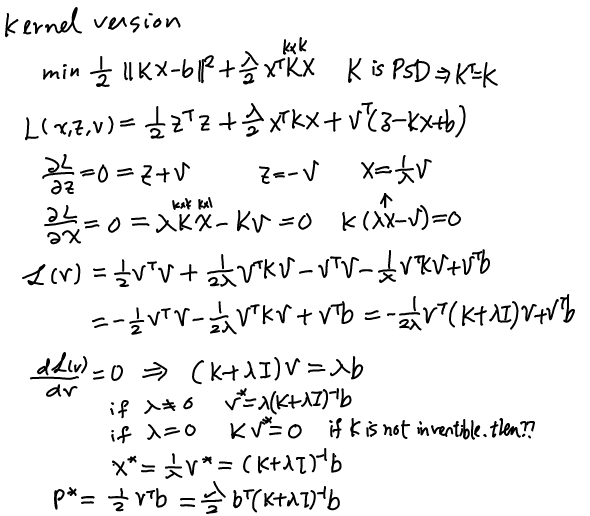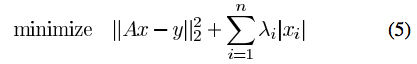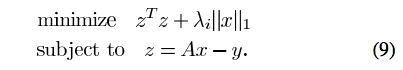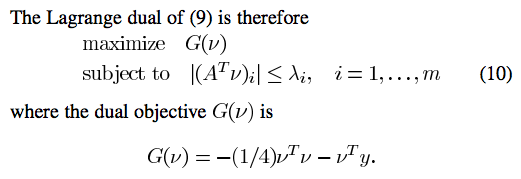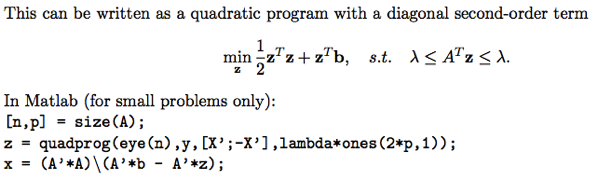本文主要參考 University of Delaware EE-636: Statistical Signal Processing and another.
前文 (Least Square and Least Norm 以及 Least Square with Regularization) 提到 LS 的公式以及應用。
主要是 data fitting (under-fit). 本文主要討論 LS 在 signal processing (filtering) 的應用。
幾點 summary:
* LS filtering 是 deterministic method.
* LS 對應 ML criterion if the error have a Gaussian distribution (之前已解釋)
* LS is related to linear regression
LS Filtering
考慮以下的 linear transversal filter (FIR filter), w (filter) 就是要 train 出的 filter.
w 是 M-tap filter. d(i) 則是 desired response (可以是事先決定的 training pattern).
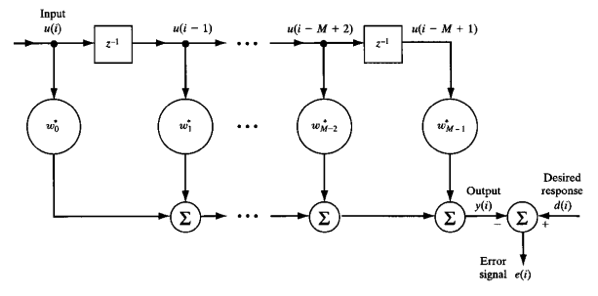
Input u(i) 是 d(i) 經過 channel model 以及 additive noise 之後的結果。
Objective: minimize
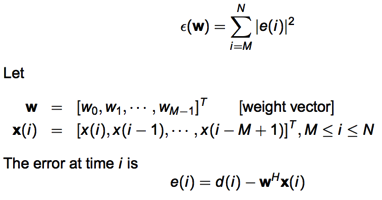
每一個 e(i) 都是 w‘ x[i] inner product 的結果。Note x[i] 是一個 vector.
LS 問題是求解 min ||Ax-b||2, w 相當於 x (short column vector, 需要求解), dim(w) = M.
A 必須是 tall matrix. Reference 用的 notation 是 minimize (d’ – w’ A’)(d – A w)
d (desired vector), 相當於 b (long column vector). 取的 size 是 (N-M+1) x 1.
為什麼不是 N x 1 而是 (N-M+1)? 因為以上 M-tap FIR filter 在初始時的 M-1 registers 都是 0, 而非 input data u(i). 需要等到 M-1 time step 之後才會得到真實的 error signal.
當然需要 (N-M+1) > M 才符合 LS 的 criterion.
M 是 features, N-M+1 是 data samples. N-M+1 > M 代表 underfit; 可做 LS.


所以 LS optimization 就是 minimize error vector 如下:

一如預期: w 是 A 的 left inverse and linear with d.
(1) 附贈 physical insight 就是 A’ ϵ(w) = A’ (Aw – d) = 0 -> Orthogonal principle or innovation process
dim(A’)=Mx(N-M+1) dim(w)=Mx1 dim(d)=N-M+1 => 以上代表 M equations=0
同時有 M 個未知 w’ = [w1, w2, …, w(M)] => 可以解出 w
e.g.
x(M).e(M) + x(M+1).e(M+1)+ .. x(N).e(N) = 0
x(M-1).e(M-1)+… + x(N-1)e(N-1) = 0
…
x(1).e(1)+ .. + x(N-M+1).e(N-M+1) = 0
where
e(i) = d(i) – w’ x(i)
意即 minimize || Aw-d ||2 = (Aw-d)’ (Aw-d) 雖然無法為 0 (因為 A 是 tall, underfit, matrix)
但至少 A’ (Aw-d) = 0!!
LS orthogonality principle: estimated error Aw-d (dim=(N-M+1)) ⊥ A’ ( M x (N-M+1) )
注意即使 A 是 fat, overfit, matrix, Aw-d=0 成立。因此 A’ (Aw-d) = 0 也成立!
因此 A'(Aw-d) = 0 is true regardless A 是 tall, square, or fat matrix.
A'(Aw-d) 稱為 innovation process, 可由導數為 0 得到。
如果 A 是 fat, overfit, matrix, 則可以找到無數多 w such that (Aw-d)'(Aw-d)=0. 此時反而要加上 regularization ( min ||w||2, Tikhonov regularization) 才能有唯一解
(2) 另一個看法是從 statistics 角度來看。w = (auto-correlation)^(-1) * (cross-correlation)
auto-correlation = A’ A (A 是 observed data matrix including noise, A’A 就是 auto-correlation)
cross-correlation = A’ d (d 是 desired output, A’ d 就是 cross-correlation)
這是非常 general 的概念: ranging from Kalman filter, MLE, …

(3) LS filter 同時也是 minimum error energy filter
因為 objective function 就是 minimize error energy function
採自前文 LS primal: p* = b’ [ I – A(A’A)^(-1)A’ ] b
b’b 是 desired energy. [ I – A(A’A)^(-1)A’ ] 是 estimation error in percentage.

再回到 orthogonality principle:

Φ 是 auto-correlation function 或是 time average correlation matrix.
Φ 是 PSD 而且一般是 PD and invertable.
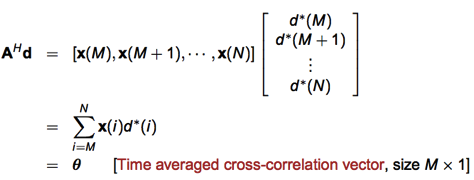

Adaptive Filter
以上提到 LS filter 的各種優點。包含 minimal error energy filter, best linear unbiased estimate (BLUE) filter, etc.
一個實務的問題是 input data 是 sequential input, 很難等到所有 data 都收集到之後才解 w (FIR filter).
另一個更重要的因素是 input data 的特性是 time-varying (e.g. wireless channel, time varying noise, etc.). 因此最佳的 LS filter 會隨著時間改變。因此 w 也應該隨時間改變,也就是 adaptive filter.
兩種常見的 adaptive filter: LS and RLS (recursive least square) based on normal equation, LMS (least mean square) based on gradient descent. LS and RLS 是 deterministic; LMS 則是 stochastic.
有兩種不同的角度來看 adaptive filter: (1) 從 statistics 角度; 以及 (2) machine learning 角度。
Statistics 詮釋
假設 desired d(i) 是一個 linear system 同時包含 unobservable measurement error (or noise).
注意 x(i) 假設是固定值,因此 A 也是固定值。但 w 因為 eo 的關係則包含 random error.

按照之前 d^ = Aw and ϵ = d – d^ => ϵ ⊥ A and ϵ ⊥ d^
下一步是 estimate bias of w^ = (A’A)^(-1) A’ d
w^ = wo + (A’A)^(-1)A’ ϵo
E{w^} = wo
cov{w^} = σ^2 * Φ^-1
where Φ = A’ A (A 是 tall matrix)
cov{w^} 和 σ^2 成正比符合預期。但和 Φ^(-1) 而非 Φ 正相關則需要思考一下。
RLS Filter

以上只是重新表述 LS filter 求解。如前所述,我們要找到一個 recursive 方法來解上述 equation.
(1) 意即 w(n+1) can be expressed in terms of w(n)
(2) 舊的 data 顯然影響力要變小。變小的幅度要可控制。這可透過 forgetting factor β 控制。重點是加在 loss/error function 中。如果 β=1 是傳統的 RLS, 只適合在 stationary statistics system. 如果 β<1 稱為 discounted or modified RLS, 可以用在 time varying statistics system.

一個常用的 forgetting factor 就是 exponential forgetting factor
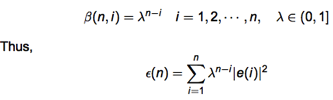
因為 error function 引入 λ, 連帶原來的 normal equation 也變成:
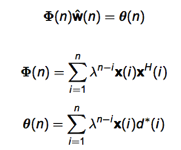

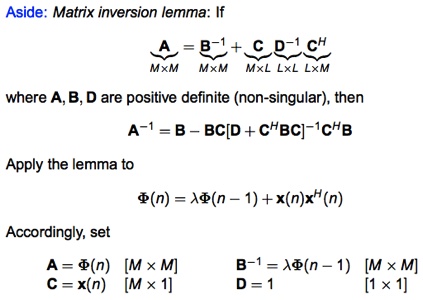

此處就有 Kalman filter 的 fu~. k(n) 類似 Kalman gain; P(n) 類似 covariance.
重點是 P(n) = Φ^(-1)(n)
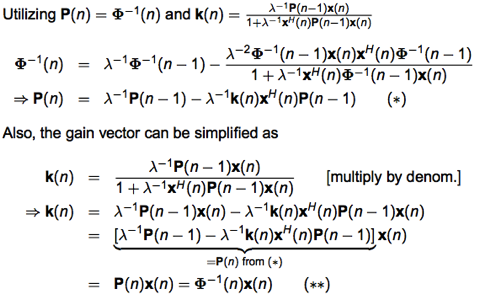


同樣用 Kalman filter analogy. α(n) 就是 prediction error; e(n) 就是 correction error.
Refresh Kalman filter 包含:
State equation:
1. X(k)=F X(k-1)+G U(k)+W(k) (covariance Q)
Measurement:
2. Z(k)=H X(k)+V(k) (covariance R)
=> F=1, G=0, H=x(n), Q=0, R = σ^2 (因為 V(k) = ϵ(k) = d(k) – x(k) w(k)’ )
=> X(k) = w(n)
=> Z(k) = d(k)
=> V(k) = Z(k) – H X(k) = d(k) – x(k) w(k) = ϵ(k) zero mean and σ^2 variance
Kalman filter 的 solution:
X(k|k-1)=F X(k-1|k-1)+G U(k) ……….. (1)
P(k|k-1)=F P(k-1|k-1) F’+Q ……… (2)
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)
Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) ……… (4)
P(k|k)=(I-Kg(k) H)P(k|k-1) ……… (5)
w(k|k-1) = w(k-1) … (1)
P(k|k-1) = P(k-1|k-1) … (2)
w(k) = w(k|k) = w(k-1) + Kg(k) (d(k) – w(k-1)’ x(k) ) … (3)
Kg(k) = P(k-1) x(k) / ( x(k)’ P(k-1) x(k) + σ^2 ) … (4)
P(k) = P(k-1) – Kg(k) x(k) P(k-1) … (5)
以上說明傳統的 RLS 是 Kalman filter 的特例。 不過 H=x(k), Z(k)=d(k) 比較出人意外。
比較 discounted RLS (with forgetting factor) 如下。
(Discounted) RLS in summary

可以看到 Kalman filter 和 discounted RLS (with forgetting factor) 有差異。
1. Equation (4) 的 𝜎^2 變為 1. 基本上是 P(n) 被 normalized 和 𝜎^2 無關。所以 R = 1??
2. Kalman filter 是處理 dynamic system, x(n+1) = A x(n) + B u(n), 只要 A and B 是準確的,就可以 track dynamic system correctly.
在一般的 RLS (λ=1) system 中,w(n) = w(n-1) + k(n) α*(n), target static system (因為 A = 1) 沒有問題。
但如果在 slowly changing dynamic system, 例如在一開始的 transient 過程,或是之後 x(n) 有些改變。如果堅持 A=1 without any dynamic factor. 可能會讓收歙的速度變慢或是 loss track. 因此引入 forgetting factor, λ. 讓最新民意佔比較大的影響力。
可以參考 recursive identification 一文。
3. Kalman filter 直觀上相當於傳統的 RLS, 所以表示 discounted RLS 比較好嗎? No. 如果用 Kalman filter 處理 dynamic system, A ≠ 1, 而應該用 position, velocity matrix, 可參考前文 (Kalman filter and water tank).
In summary:
-
Kalman filter: Track a moving object (estimate its location and velocity at each time), assuming that velocity at current time is velocity at previous time plus Gaussian noise). Use a sequence of location observations coming in sequentially.
-
Recursive LS: Keep updating estimate of location of an object that is static. Use a sequence of location observations coming in sequentially.
-
Discounted Recursive LS with forgetting factor: object not static but drifts very slowly.
LMS Filter
RLS filter 雖然看來有很多優點: (1) Recursively (不需要等所有 data samples); (2) adaptive tracking dynamic change (with forgetting factor); (3) Computation ~ M^2, 已經比 LS ~ M^3 好很多,但在 feature space (M) or FIR tap 大的時候,非常慢。
但 RLS 最大的缺點: (1) computation 量大,需要計算 matrix inversion; (2) stability and 收歙性的問題。
LMS filter 最大的好處是 computation 少很多。同時只需要 local information, 也非常 robust to model error, noise, etc.
說 LMS 之前,必須先談 gradient descent (GD). GD 也是需要等所有 data samples 才能計算。實務上也不可能。因此才有 LMS, 對應 stochastic gradient descent.
wo = Φ^(-1) θ where Φ is auto-correlation; θ is cross-correlation
GD, LMS 基本上都不用 matrix inversion 來算 w. LS, RLS 則是需要計算 matrix inversion (or simplified algorithm 來算 w.

再重覆之前的推導:
e(n) = d(n) – d^(n) = d(n) – w(n)’ x(n)
MSE at time n
J(n) = E{|e(n)|^2} = σd^2 – w(n)’ p + p’ w(n) + w(n)’ R w(n)
where
σd^2 – variance of desired signal
p – cross-correlation between x(n) and d(n)
R – auto-correlation matrix of x(n)
對這 quadratic function 的 optimal (Wiener) solution,
w(n) = wo = R^(-1) p
J(n) = Jmin = σd^2 – p’ wo = σd^2 – p’ R^(-1) p
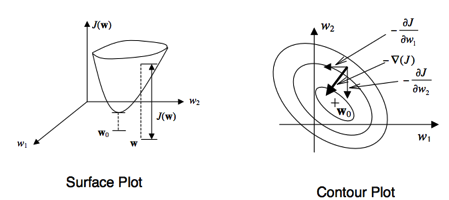
如何能在不計算 matrix inversion (R^(-1)) 情況下,仍能求得最佳的 w* 以及 J*?
1. 前述如果要等全部 data ready (R and p) 才做 matrix inversion, 在實務上很多時候不可行。
2. 解決方法之一是 recursive LS. 可以每多一個 data sample 就 update w. 就像 Kalman filter. 最大的問題是仍需要算 matrix inversion (recursively), computation 量還是太大。同時也要 a priori error surface (global information).
解決之道是只用 local information, iteratively approach optimal solution 如上圖 contour plot.
w(n+1) = w(n) + 1/2 μ [-∇J(n)]
∇J(n) = -2p + 2 R w(n)
w(n+1) = w(n) + μ [ p – R w(n) ] where μ 是 step size, 或是 learning rate
μ 太大有可能 unstable; μ 太小則收歙慢。
μ 必須小於 eigenvalue of R 才能 guaranteeing stability (Widrow).
有一整套的理論如何選取 μ 以及其他 的參數,可以參考本文。
我們可以從 machine learning 角度來看 adaptive filtering.
基本上是 linear regression with least square loss function.
可以引入 learning rate concept.
有兩種做法,recursive and stochastic gradient descent, 對應的就是 RLS 和 LMS.
Difference Between RLS or LMS
首先是算法本身。RLS 是 based on a priori error; LMS 是 based on a posteriori error.
RLS 的 gain 是 based on minimize least square error; LMS 的 μ 則是比較 heuristics.

再就 algorithm 本身的複雜度比較 (M 是 FIR filter tap number; or feature dimension in machine learning).
LMS:

LS:

RLS:

Andrew Ng 做了一個簡單的比較。 Normal equation 主要是指 LS, 不過也適用 RLS.
Gradient descent 是指 LMS. 另一個重點是 gradient descent 可用於各種 loss function (square loss, L1 loss, hinge loss, cross-entropy loss). Normal equation 主要是 square loss!
所以 gradient descent, e.g. LMS 算法非常重要。

LMS -> learning is done by stochastic gradient descent
RLS -> Recursive least square -> iterative gradient descent
1. Signal recovery problem: Wiener fileter
2.
LS with L2
iterative filter
Kalman filter
Wiener filter
LMS
Physical meaning of primal and dual