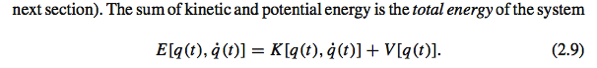Reference
Chapter 2: Geometry of Hamiltonian Mechanics (in Dropbox differential geometry)
Wiki : Hamiltonian mechanics
Tips: 可以推廣到 4D space-time coordinate!
Analytical Mechanics vs. Newton Mechanics
我在學 analytical mechanics (i.e. Lagrangian mechanics or Hamiltonian mechanics) 一直有一個問題。
就是 generalized coordinates in Lagrangian or generalized postion, q, or generalized momentum, p, in Hamiltonian.
引入 generalized coordinate 很自然。因為某一些 constraints (如單擺), 使用 polar coordinate 絕對比 Cartesian coordinate 更簡潔。
問題是為什麼 Lagrangian differential equation or Hamiltonian equation 可以只對 generalized coordinate (r, r_dot, θ, θ_dot) 做偏微分? 而非對 (x=rcosθ, y=rsinθ, x_dot, y_dot) 或是對 (r, r_dot, rθ, (rθ)_dot) 做偏微分。
任何阿狗阿貓都可以當 generalized coordinate 嗎? 非正交 coordinate 也可以嗎 (雙擺的 θ1, θ2 顯然非正交)? 等等問題。
另外 Lagrangian/Hamiltonian mechanics 比起 Newtonian mechanics 的好處 (1) scaler vs. vector equations, 不用找力更簡潔; (2) generalized coordinates 在 constraint system (如單擺) 更簡潔; (3) 除了使用在 particle physics 之外,Lagrangian/Hamiltonian 也可以用在 field (EM field) 上。 還有其他的好處嗎?
Yes. 很多書或 wiki 都提到 (4) Lagrangian/Hamiltonian mechanics 可以直接 transform 到 relativistic mechanics (curved space-time mechanics) 和 quantum mechanics (operator mechanics or Poisson bracket).
Lagrangian 和 Hamiltonian 的差別?
另外一個問題是 Lagrangian 和 Hamiltonian 的差別到底在那裡? 一般說法是 Lagrangian equations 是 N 個 2nd order differential equations. Hamiltonian equations 是 2N 個 1st order differential equation. Hamiltonian 更好的展示 intrinsic symmetry. 但有更直觀的解釋這兩者的差別嗎? Lagrange 是偉大的數學物理學家,他沒有看到什麼更深的東西?
Lagrangian 和 Hamiltonian 是 Legendre transform pair. 但這只是代數的結果 (algebra). 是否有更直覺的解釋 ( Geometry?) –> covariant vs. contravariant –> Wrong, Tangent space vs. Cotangent space.
YES!!!!!! 就是 Geometry of Hamiltonian mechanics.
Differential Geometry View for Mechanics
前文提到學 differential geometry 的 path:
* Tensor calculus (in Euclidean space first, then manifold embedded in Euclidean space, then curved space)
* Differential geometry on manifold
* Advanced topic (Riemannian geometry with connection, geodesic, flow; information geometry)
Step 1:
Euclidean space:
首先 tensor calculus or differential geometry 最重要的特性就是 coordinate free!!! 利用 coordinate , 但不要 pick any specific coordinate. 特別是 Cartesian coordinate!!! 結果必須 apply to all coordinate systems.
這和 generalized coordinate 的想法不謀而合。Spell everything in local basis. everything needs to work in different local basis (Cartesian coordinate 所有 local basis is the same).
Lagrangian 和 Hamiltonian 的差別就是 covariant basis and contra variant basis!! –> Yes
另一個說法: 差別是 tangent space and cotangent space (?)
Step 2:
Manifold in Euclidean space:
Constrained mechanics 可視為 manifold in higher dimension Euclidean space! Generalized coordinate 就是 local bases (defined by partial derivative of position vector).
Lagrangian 就是 manifold 上的 geodesic.
Hamiltonian 就是 manifold 上的 Hamiltonian flow.
Step 3:
Curved space-time:
Apply Lagrangian and Hamiltonian in curved spacetime.
Cartesian Coordinates without Constraints
考慮 N particles system in a 3D Cartesian coordinate system, described by N vectors.
整個運動方程式可視為 N particles in 3D space, 或是等價於 1 particle in 3N-dimension space.
如果沒有任何 constraints, total DOF (degree of freedom) 是 3N. 可視為 3N-dimension (Euclidean) manifold (M), 不需要 embedded 在更高維的 Euclidean space.
我們可以用 Cartesian coordinate describe 如下:



當然 differential geometry 的精神就是 coordinate free. 不一定要用 Cartesian. r, v, 都是 tensor.
K 是 invariant (?), 也是 0-th order tensor.
F 也是 tensor? Tensor 可以用 Jocobain 做座標轉換。
不過 pick different coordinate 在 constraints 時更有用如下。
Curvilinear Coordinates (with Constraints)

舉例而言,如果單擺則 r = length (a constant); but θ is a free parameter.
此時的 DOF 變成 3N – k = n (dimension). 就是新的 manifold Q of dimension n (=3N-k). 注意新的 manifold 不一定是 Euclidean; 事實上大多不是 Euclidean manifold.

此時我們導入 n 個 DOF as generalized coordinates, (q1, q2, …, qn).

再導入 generalized velocities (or momentum) (q’1, q’2, …, q’n)

重點是 gik(q,m) 對應的是 differential geometry 的 metric tensor.
如果沒有 potential energy, Principle of least action 要 optimize 的 action 只有 kinetic energy. 因此 least action principle 對應的就是 differential geometry 的 geodesic curve on the configuration manifold!!
如果有 Potential energy, V, 就會有兩個量: Lagrangian and total energy (也就是 Hamiltonian).
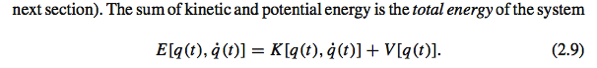
此時的 principle of least action 對應的 action 是 Lagrangian, 為何不是 Hamiltonian?
以下說明:
Topological Map of Lagrangian and Hamiltonian Mechanics
Topological theory 乍看之下是定性的結論,和 mechanics 有距離,因為 mechanics 需要 metric, time, 等 rigid 觀念。不過 differential geometry 是把 topological space/map 和 metric 等結合。只是不 pick 特定的 coordinate systems. Lagrangian and Hamiltonian mechanics 對應兩種不同的 topological map, 主要是不同的 local coordinate systems.
重點就是 potential function V is a map of configuration manifold to real number R. V: Q -> R. 在 tangent bundle we can define state function 就是 Lagrangian.


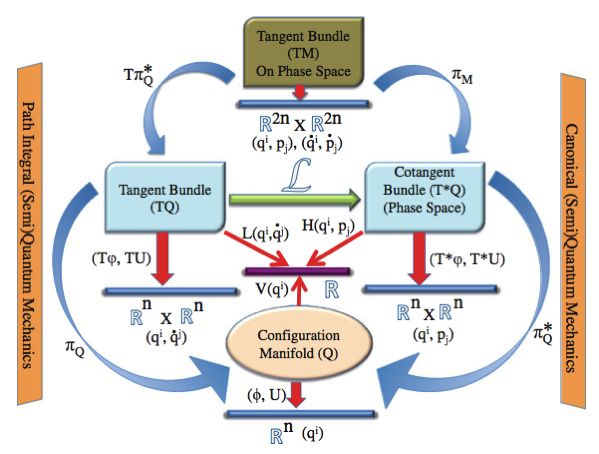




p 看起來像是 q_dot 的 contravariant bases.

p and q_dot 是 covariant and contra variant bases. 由 metric tensor gs link 在一起 (?, yes)

(q, p) 是 manifold Q 加上 cotangent space T* => cotangent bundle => phase space
結論: q 是定義 n-dimension manifold. q_dot (不含 V) 和 p (不含 V, 因為是對 q_dot 導數) 是定義 tangent space and cotangent space.
在 V=0 的情況下, L = H = K(q, q_dot). Principle of least action (PLA) 的 Lagrangian 等價於 geodesic. Hamiltonian 相當於 flow.
但 V ≠ 0. Hamiltonian 相當於 flow 仍適用。但 Lagrangian 等價於 geodesic 嗎? NO!
q 仍然一樣。q_dot 仍然一樣。但 p 是從 Lagrangian 對 q_dot derivative definition 而來,不包含 V.
所以 V 到底扮演什麼角色??????? 唯一的角色是 (2.21) generalized force. 如何融入 differential geometry interpretation? 在 manifold (No), tangent space(No), cotangent space (No), metric tensor(No).
Principle of Least Action (PLA)
Lagrangian and Hamiltonian 基本上都是 based on PLA. 可以說 PLA 是比 Newton 力學定律更 fundamental 的自然規律。
Action 就是 differential Lagrangian. 從變分理論可以導出 Euler-Lagrangian equation. 等價於 Newton 第二定律, done.
但是 Hamiltonian 又如何? Hamiltonian (energy) 是一個常數 (能量守恆), 如何用來做 least action?
重點在於 Hamiltonian flow. Hamiltonian 是常數對應在 phasor plane 是封閉的 contour. 可以証明對應的 flow 是 uncompressed, 不會相交, 面積 (2D) or 體積 (3D) 永遠一致。
對應在 differential geometry 上: Lagrangian (without potential, V=0) 是找 q(A) 到 q(B) 點的 geodesic curve on the manifold (what if V is not 0? 也是 geodesic 嗎?). 非常直觀。 Hamiltonian 似乎是連結 constant energy function on the manifold from q(A) 到 q(B) on the manifold.
上述的 differential geometry geodesic (Lagrangian) or flow 成立的前提是 L and H not explicitly depending on t!!!
Lagrangian and Hamiltonian 是在同樣的 manifold 嗎? Yes, –> but different tangent and cotangent space.
Lagrangian without potential 是 Geodesic 的說明:
以下 x 就是上文的 q (generalized coordinate).
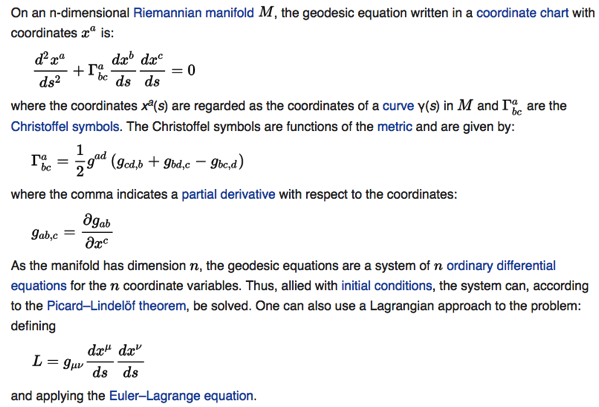
再多說明。V=0, PLA 對應 manifold 的 geodesic curve. 如果加上 V(q) (potential field) 會扭曲 geodesic curve. 舉例而言,在有重力場的情況下,會改變 q(t). 當然在 Einstein general relativity 中, 重力直接改變 spacetime 的 curvature.


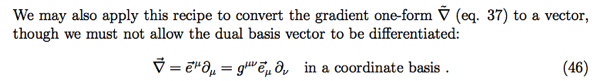
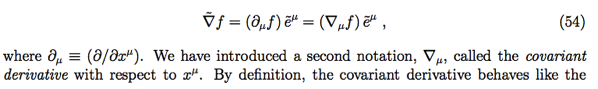
![]()
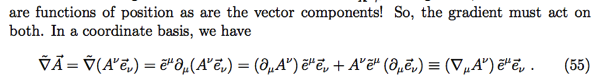
![]()
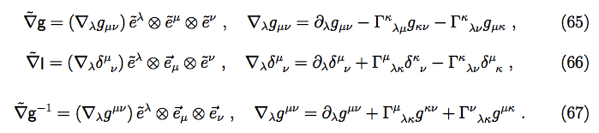
![]()
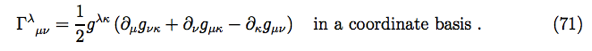
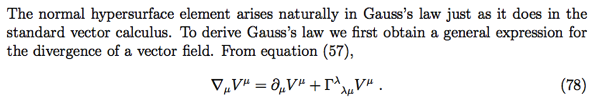

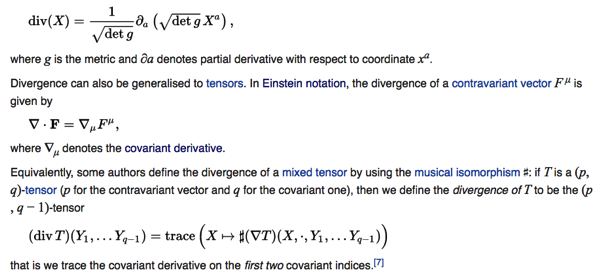
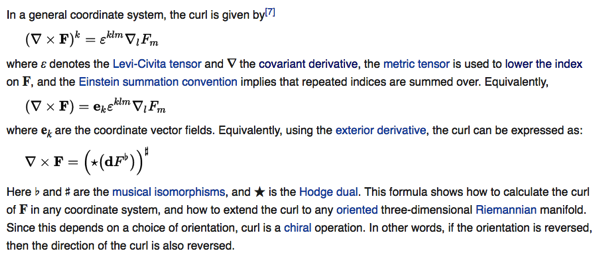
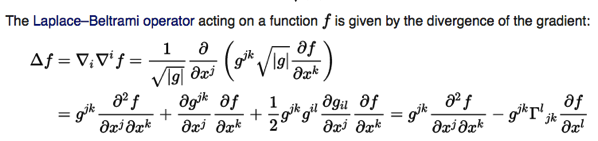
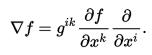
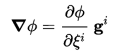 using Einstein notation.
using Einstein notation.