Parameter Estimation 參數估計

by allenlu2007

What is Parameter Estimation

參數估計是指用樣本指標(稱為統計量)估計總體指標(稱為參數)。例如用樣本 mean 估計總體 mean 以及用樣本 variance 估計總體 variance。

Parameter Estimation 分類

Parameter estimation 有點估計 (point estimation) 和區間估計 (interval estimation) 兩種。

點估計是依據樣本估計總體分佈中所含的未知參數或未知參數的函數。通常它們是總體的某個特征值，如數學期望、方差和相關係數等。點估計問題就是要構造一個只依賴於樣本的量，作為未知參數或未知參數的函數的估計值。例如，設一批產品的廢品率為θ。為估計θ，從這批產品中隨機地抽出N個作檢查，以X記其中的廢品個數，用X/N估計θ，這就是一個點估計。

點估計常用的方法是：

　　(1) Classic estimation:   特征值參數θ是一個定值 (non-random), 同時沒有任何先驗資訊 (a priori information).  例如 Maximum likelihood 最大似然估計法。於1912年由英國統計學家 R.A. Fisher 提出，利用樣本分佈密度構造似然函數來求出參數的最大似然估計 (Maximum likelihood estimation)。

　　(2) Bayesian estimation: 基於貝依氏學派的觀點而提出的估計法。特征值參數θ是一個 random variable, 同時允許 a priori PDF on θ.  例如 Maximum a posteriori (MAP) estimation, 或是 Minimum mean square error (MMSE) estimation.

區間估計是依據抽取的樣本，根據一定的正確度與精確度的要求，構造出適當的區間，作為總體分佈的未知參數或參數的函數的真值所在範圍的估計。例如人們常說的有百分之多少的把握保證某值在某個範圍內，即是區間估計的最簡單的應用。1934年統計學家 J. Neyman 創立了一種嚴格的區間估計理論。本文只討論點估計的 parameter estimation.

Bayesian Parameter Estimation

Given the conditional pdf

p({y}_{1}, ..., {y}_{N}|x) = p(\mathbf{y}|x)

以上 {y}_{1}, ..., {y}_{N} 是實驗值。以及 x 是被估計的參數 (unknown)，根據貝依氏的理論是一個 random variable.

再來定義 \hat{x} 是 x 的 estimator, 以及估計的誤差

\epsilon_x = x - \hat{x}(\mathbf{y})

Cost Function and Bayes Risk

貝依氏參數估計的重點就是引入一個 cost function c(\epsilon_x), 或 loss function.   注意 cost function 仍是一個 random variable.

我們稱 cost function 的期望值為 Bayes risk, R relative to the joint pdf p(\mathbf{y}, x) .

R = E[c(x-\hat{x}(\mathbf{y}))] = \int \int c(x-\hat{x}(\mathbf{y})) p(x,\mathbf{y}) dx d\mathbf{y}

貝依氏的參數估計就是 minimize Bayes risk R.

以下舉幾個 cost function 的例子以及 Bayes estimation 如何 link 到常見的 estimator.

Quadratic cost function (如下圖一):

{c}_{q}({\epsilon}_{x}) = {{\epsilon}_{x}}^{2}

Uniform (binary) cost function (如下圖二):

{c}_{u}({\epsilon }_{x}) = \begin{cases} &0 \text{ if } |{\epsilon }_{x}| \leq \frac{\delta }{2} \\ &1 \text{ if } |{\epsilon }_{x}| > \frac{\delta }{2} \end{cases}

NewImage

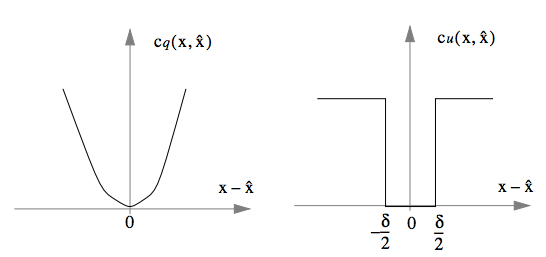
Minimum Mean Square Error (MMSE) Estimator

MMSE estimator 對應為 quadratic cost function.  Bayes risk R:

R_q = E[c(x-\hat{x}(\mathbf{y}))] = \int \int (x-\hat{x}(\mathbf{y}))^2 p(x,\mathbf{y}) dx d\mathbf{y}

可以用 Bayes formula 簡化上述公式

R_q = \int d\mathbf{y} p(\mathbf{y}) \int (x-\hat{x}(\mathbf{y}))^2 p(x|\mathbf{y}) dx

Since both integrals are not negative, minimize risk R_q 相當於 minimize

\int (x-\hat{x}(\mathbf{y}))^2 p(x|\mathbf{y}) dx

可以証明

\hat{x}_{MMSE} = \int x p(x|\mathbf{y}) dx = E[x|\mathbf{y}] 


Maximum A Posteriori (MAP) Estimator

 NewImage

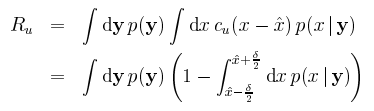
To minimize Ru 相當於 maximize the following integral.

NewImage

\hat{x}_{MAP} = \arg \max_{x} \log p(x|\mathbf{y})

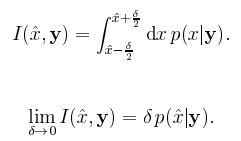
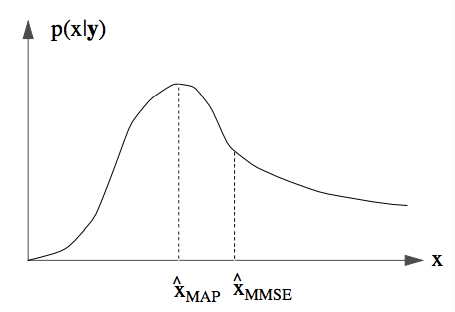
可以觀察到  MMSE 和 MAP estimators 都用到 posterior pdf p(x|\mathbf{y}).

MMSE 是 center of mass, MAP 是 mode (peak) of pdf.  如果 conditional pdf is symmetric posterior pdf the MMSE and MAP estimators are equal.


What’s the difference between Cramer Rao bound and MMSE estimator??

NewImage

Maximum Likelihood (ML) Estimator

考慮一個特例, x 是未知但定值 (unknown but deterministic). 這其實是 classic estimation, 是否能用以上 Bayesian estimation 解釋？

NewImage

NewImage

\hat{x}_{MAP} = \arg \max_{x} \log p(x|\mathbf{y})

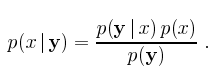
可以簡化為

\hat{x}_{MAP} = \arg \max_{x} \log p(\mathbf{y} | x)

這是 Maximum likelihood estimator. 

當然從 classic estimation 角度，出發點完全不同。通常我們先把 x (random variable) 換成 \theta (non-random variable).  再定義 likelihood function L, ML estimator 即是找 Likelihood function maximum.   或是 Log-likelihood function maximum.

L(\theta | \mathbf{y}) = p(\mathbf{y} | \theta )

\frac{\partial \log L(\theta | \mathbf{y})}{\partial \theta } = 0

\hat{x}_{ML} = \arg \max_{x} \log p(\mathbf{y}|x)

所以 MAP estimator 根據 Bayes formula 可以改寫為

\hat{x}_{MAP} = \arg \max_{x} \log p(\mathbf{y}|x) p(x)

Remark

如果 p(x) is uniform distribution (此為充分條件，非必要條件), MAP 和 ML estimators 相同。

 NewImage

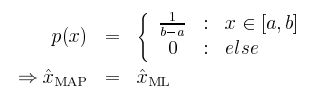
其實這正反應了 ML estimator 完全 no prior information of x, 所以才會是 uniform distribution (不管 x 在那的機會均等).  如果我們事先知道 x 的 pdf (非 uniform distribution), 就變成 MAP estimator, 理論上可以最更好的 estimation (假設 prior information 是準確的)。  這也是 Bayesian estimator 的精神所在。


 

Maximum Mean Absolute Value of Error (MAVE) Estimator

NewImage

 

 NewImage

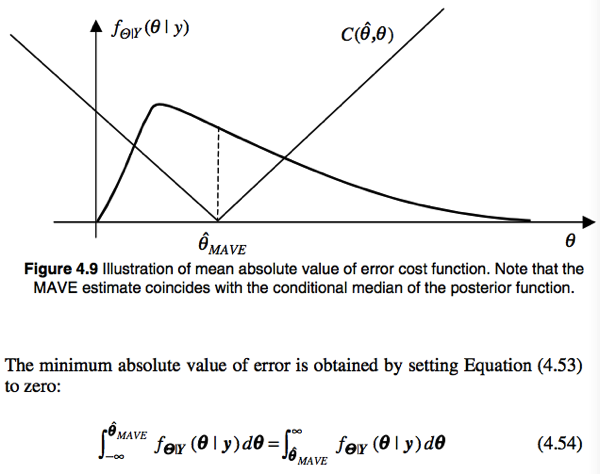
From the above equation MAVE estimator is the median of the posterior density.