Tensor IIB – 微分
by allenlu2007
Tensor Differentiation, 包含 Gradient
Gradient of tensor (n, m) –> (n, m+1)
看具體的例子
Scalar: type (0, 0), f
Gradient of scaler : (0, 0) –> (0, 1) 變成 1-form!!
![]()
再來是為什麼是 1-form?
一個解釋是 directional derivative using a curve: e.g. f( x(t), y(t) )
df = grad( x, y) * (dx, dy) dt ==> scalar
因為 (dx, dy) 是 vector ==> grad(x, y) 是 1-form
Covariant derivative
再來就是有名的 covariant derivative, 就是 gradient of a vector, type (1, 0) –> type (1, 1) Yes!!
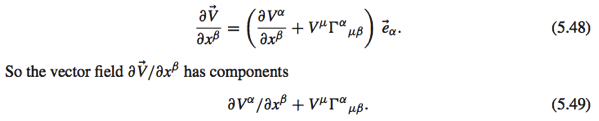


or
![]()
![]()
注意 scalar 的 covariant derivative = partial derivative!!
幾何上 p 是同一點。和 vector 的不同點不同。
代數上因為 微分包含 basis vector 的微分
同樣 covariant derivative of 1-form (0, 1) –> (0, 2)


Scalar: type (0, 0), 但是用 <p~, v> where p~ is 1-form, v is a vector
grad <p~, v> …. => reference Schutz book!!
再來考慮 gradient of tensor (2, 0), (1, 1), and (0, 2)

一個重點是 gradient of g, g^-1, (of course I) 為 0!!! 因為可以找到 local 平面。但 2nd derivative 不為 0, 可以定義曲率!
![]()
Divergence (另一種微分 and summation)
Differentiation of Tensor